一团乱麻的电

事情要从那一团看不见、摸不着，但偶尔会把你手指尖打得生疼的东西说起。

时间回到 18 世纪中叶。那时候的电学，与其说是一门科学，不如说是一场表演。宫廷里的贵族们穿着丝绸衣服，在摩擦起电的机器旁排着队，等着体验那种酥酥麻麻的刺痛感。他们惊叫、大笑，他们觉得这玩意儿比下午茶有趣多了。莱顿瓶（那个能储存电荷的玻璃罐子）刚刚被发明出来，人们发现如果把这东西串联起来，能把一整队手拉手的士兵电得同时跳起来。

大家都很开心，除了那些真正的物理学家。

此时的物理学界正陷入一种深深的焦虑。艾萨克·牛顿已经在前一个世纪把万有引力定律甩在了桌面上，告诉大家宇宙是有秩序的，力与距离的平方成反比。重力是如此优雅，如此精确，只要你给出一个质量，给出一个距离，算式就在那里，不偏不倚。

可是电呢？它有时候吸引，有时候排斥。它受天气影响，潮湿一点它就消失了，干燥一点它就到处乱窜。并没有人知道两个带电体之间的力到底有多大。大家只知道“离得越近，劲儿越大”，但这算什么定律？

那时候的电学论文画风清奇。科学家们在论文里写道：“我把带电的玻璃棒凑近羽毛，羽毛飞快地跑了，真的很神奇。”或者是：“火花有两英寸长，蓝色的，很漂亮。”

没有公式。没有数字。没有精确的测量。只有定性的描述和一堆关于“电流体”的哲学猜测。本杰明·富兰克林虽然聪明地提出了正电和负电的概念，把一团乱麻稍微理出了一点头绪，但他也没法告诉你，两个正电荷之间那个要把对方推开的力，到底是多大。

每个人都想找到那个公式。大家都猜那个公式应该长得像万有引力定律。约瑟夫·普利斯特里，就是那个发现氧气的科学家，他在 1767 年就猜到了。他注意到带电金属杯内部没有电力，这和万有引力在球壳内部为零的数学推导很像，于是他大胆推测：电力也遵循平方反比定律。

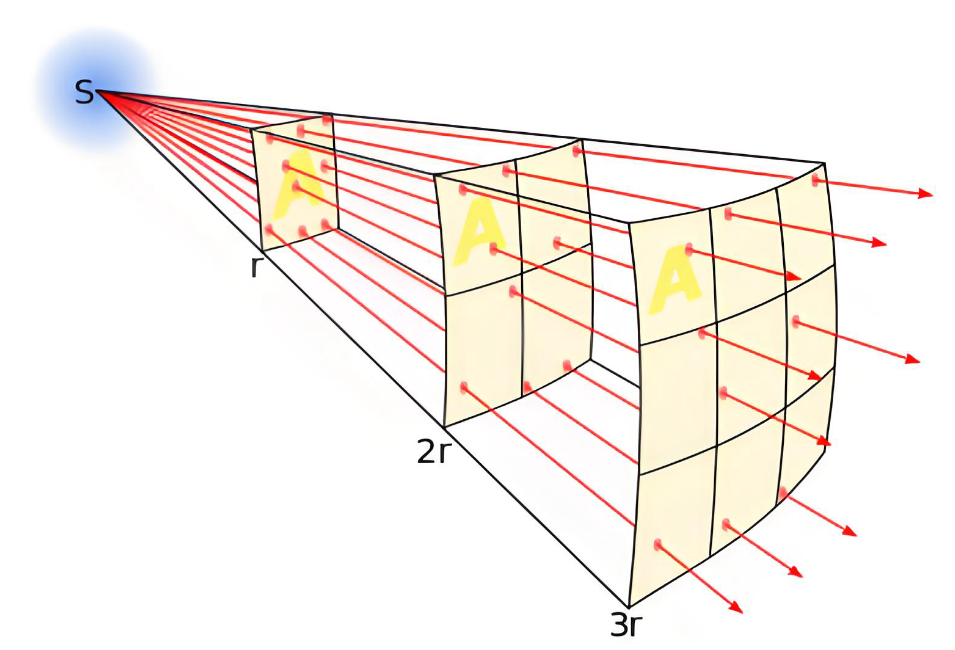
但也只是猜测。

猜测在物理学界不值钱。你得证明。你得拿出一组数据，画出一条曲线，然后把那个公式写下来，还要保证任何人在任何地方只要照着做，结果都一样。

这太难了。

重力好测量，因为地球就在这儿，苹果就在这儿，质量是稳定的。但电荷会泄露。你刚给一个小球充上电，空气里的灰尘、支架上的微小湿气，甚至你呼吸出来的水汽，都在偷偷地把电荷运走。你还没来得及读数，力就已经变了。

而且那个力太小了。两个带电小球之间的力，微弱到连一只蚊子的呼吸都比它重。你要怎么在一个充满振动、气流和静电干扰的世界上，测量这么微弱的一个力？

这需要一个对精度有着病态追求的工程师。查尔斯·奥古斯丁·德·库仑登场了。

修碉堡的工程师

库仑其实不是个纯粹的理论物理学家。在很长一段时间里，他的工作是修碉堡。

他毕业于皇家工程学院，是个正儿八经的军事工程师。他在马提尼克岛待了九年，那是加勒比海上的一个法国殖民地。他在那里干什么呢？指挥工人们搬石头，计算土墙的压力，设计防御工事的结构。听起来和电学风马牛不相及。

但正是这段经历塑造了他。在马提尼克岛，他不仅要和热带的疟疾作斗争，还要解决非常实际的工程问题：一根梁能承受多大的力？一堵墙会不会被土压垮？摩擦力到底是怎么回事？

特别是摩擦力。这是工程师的噩梦，也是物理学家的盲区。

为了搞清楚摩擦和扭转，库仑在 1777 年回到法国后，参加了巴黎科学院的一个悬赏竞赛。题目是关于制造航海罗盘的。为了让罗盘的指针灵敏，必须减少轴承的摩擦。库仑想了一个办法：为什么要用轴承呢？为什么不把针悬挂在一根细丝上呢？

当他研究这根悬挂的细丝时，他发现了一个惊人的现象。

如果你用一根金属丝悬挂一个物体，然后转动那个物体，金属丝就会产生一个反抗的力矩。库仑通过无数次枯燥、重复、极其考验耐心的实验，确立了一个定律：金属丝扭转时的反抗力矩，与扭转的角度成正比。

这就是胡克定律在扭转上的应用。但这不仅仅是一个定律，这是一把钥匙。

这把钥匙可以打开微观力学的大门。

你想想看，如果你想测量一个力，通常你会用天平。天平的一端放物体，另一端放砝码。但如果那个力比最小的砝码还要小一千倍怎么办？

库仑看着那根细细的金属丝，心里有了主意。如果那个微小的力能推动一根悬挂的杆子转动一点点角度，而我知道这个角度对应多大的扭转力矩，那我不就知道了那个力的大小了吗？

1785 年，库仑已经是一个 49 岁的中年人了。他带着他的新发明——扭秤，走进了电学的战场。他要挑战那个没人能解开的问题：电荷之间的力，到底遵循什么规律？

玻璃罐里的精细活

库仑的这个装置，是一个玻璃圆筒，大概 12 英寸宽，12 英寸高。玻璃是为了挡风。在这个尺度的测量里，你打个喷嚏产生的气流就能毁掉整个实验。圆筒上面盖着一块玻璃板，板中间立着一根玻璃管。

在玻璃管的顶端，有一个可以转动的测微计。从测微计的中心，垂下来一根丝。

这根丝是整个装置的灵魂。它是一根银丝，细得像头发一样。库仑甚至尝试过用极细的金丝。这根丝的下端，悬挂着一根横杆。横杆是用涂了火漆的麦秆做的。为什么用麦秆？因为它极轻，而且绝缘。

在横杆的一端，粘着一个木髓球。这是一种像泡沫塑料一样轻的植物材料。为了平衡，横杆的另一端有一个平衡球。

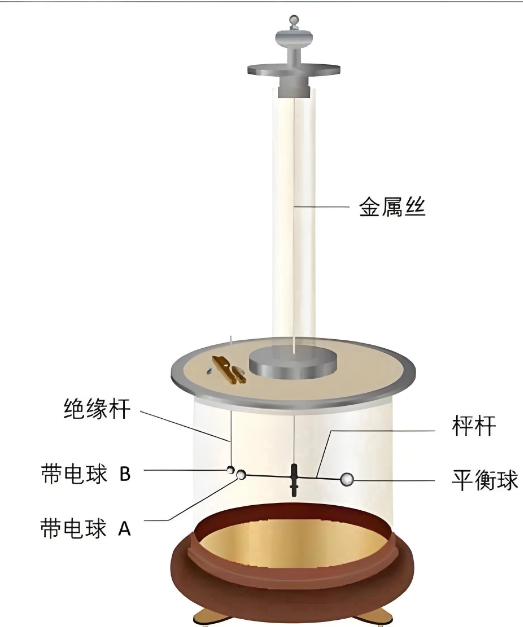
这就是全部的活动部件。一个悬在银丝上的麦秆和木髓球。

现在，实验开始了。

库仑先把那个悬挂的木髓球（我们叫它球 A）调整好，让它静止。然后，他拿出一根绝缘棒，棒头带着另一个一模一样的木髓球（我们叫它球 B）。

他给这两个球带上同种电荷。怎么带？很简单，让它们接触一下带电体就行。

然后，他把球 B 通过玻璃盖上的一个小孔，插进瓶子里，让它去接触悬挂着的球 A。

就在接触的一瞬间，奇迹发生了。

因为两个球带上了同种电荷，它们开始互相嫌弃。电荷的斥力把球 A 推开了。球 A 带着横杆开始旋转。银丝被扭紧了。

球 A 转啊转，直到银丝扭转产生的反抗力矩，和两个球之间的电斥力达到平衡。这时候，横杆停下来了。

库仑凑近玻璃瓶，眼睛盯着刻度。他读出了一个角度：36 度。

这时候，银丝扭转了 36 度。这个 36 度，就代表了此时此刻，两个球在相距一定距离时的斥力大小。

但这只是第一步。这只是知道了“现状”。为了找规律，库仑必须改变距离，看看力怎么变。

这就是这个实验最反直觉、也是最精彩的地方。通常我们做实验，是改变距离，测量力。但库仑的扭秤反其道而行之。他通过旋转顶部的测微计，强行扭转银丝，把球 A 往回推，逼着它去靠近球 B。

他在和电斥力较劲。

库仑转动顶部的旋钮，银丝被扭得更紧了。那个力矩通过银丝传导下去，逼迫球 A 克服电斥力，向球 B 移动。

他扭啊扭，直到球 A 和球 B 的角距离缩小了一半，变成了 18 度。

这时候，他看了一下顶部的旋钮。他转了多少度？他惊人地发现，他不得不把旋钮转过 126 度。

加上底部的 18 度，银丝总共扭转了 144 度。

停下来算一算。

距离从 36 度变成了 18 度，距离缩小为原来的二分之一。

力（也就是扭转角）从 36 度变成了 144 度。36 乘以 4 等于 144。

力变大了 4 倍。

距离减半，力变四倍。

库仑没有停。他继续转动旋钮，在那根脆弱的银丝断裂之前，他把球 A 逼得更近。直到两个球的距离只有 9 度左右。距离差不多是最初的四分之一。

这时候，银丝的总扭转角达到了惊人的 575 度左右。

575 除以 36，大约是 16。

距离变为四分之一，力变为十六倍。

数据就在那里，赤裸裸地摆在库仑面前。哪怕有漏电的干扰，哪怕有读数的误差，那个趋势也强硬得像一块石头：斥力与距离的平方成反比。

他在实验室里，看着那个封闭的玻璃罐子。罐子里的两个小球静静地悬在那里，维持着一种紧张的平衡。看不见的电场在它们之间推搡，而那根银丝忠实地记录下了这一切。

这就是著名的库仑第一定律：同性电荷相斥，斥力与距离的平方成反比。

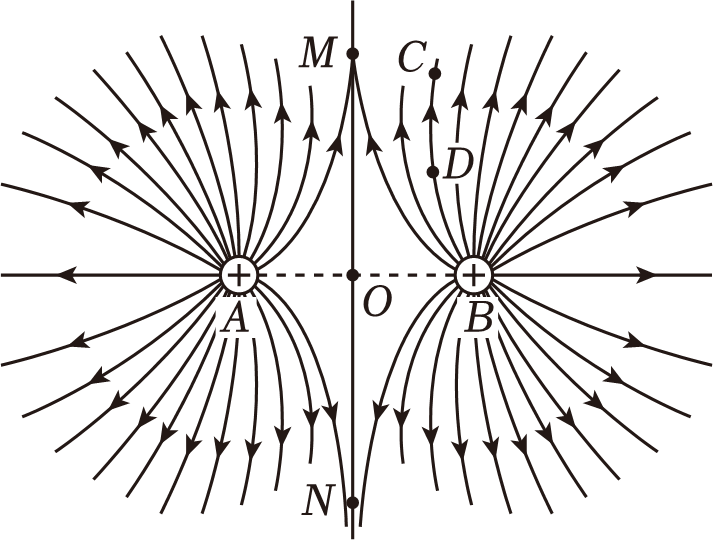
电的引力

斥力搞定了。但是引力呢？

异性电荷相吸。这听起来似乎只要把上面的实验反过来做就行了。找两个带异种电荷的球，看它们怎么吸。

如果你真这么想，那就错了。

测量引力是库仑的噩梦。

在斥力实验中，如果你把球推近一点，斥力会变大，试图把你推回去。这叫稳定平衡。就像在碗底放个弹珠，你推它一下，它还会滚回来。

但在引力实验中，两个球互相吸引。如果你不小心让它们靠得太近，引力会突然暴涨，两个球就会“啪”地一声撞在一起。这叫不稳定平衡。就像在针尖上立鸡蛋，稍有风吹草动，实验就毁了。两个球一旦接触，电荷就会中和或者重新分配，一切都得重来。

用扭秤测量引力，是不靠谱的。库仑试了几次，发现这太难控制了。扭秤太灵敏，灵敏在这里成了缺点。

库仑必须换个思路。他是个工程师，工程师最擅长的就是：此路不通，就绕路。

他想到了单摆。

如果你推一下秋千，秋千会摆动。秋千摆动的快慢（频率），取决于地球的重力。重力越大，把它拉回低点的力越大，它摆动得就越快。

库仑做了一根绝缘针，像指南针一样悬挂起来。他在针的一头带上电。然后，他拿另一个带异种电荷的球，放在离针一定距离的地方。

这个固定的球会吸引针头。如果我们把针头稍微拨开一点，它就会在电引力的作用下开始摆动，就像秋千在重力作用下摆动一样。

库仑只需要拿着秒表，数针头摆动的次数。

如果电引力也遵循平方反比定律，那么当距离减半时，力应该变为 4 倍。力变为 4 倍，摆动的频率（单位时间的摆动次数）应该变为 2 倍（因为频率与力的平方根成正比，这是力学常识）。

于是，库仑开始数数。

距离 d 时，摆动 15 次用了 20 秒。

距离 d/2 时，摆动 15 次用了 10 秒。

距离 d/4 时，摆动 15 次用了 5 秒。

时间减半，意味着频率加倍。频率加倍，意味着回复力变成了 4 倍。

完美。

无论是推开还是拉近，不管是斥力还是引力，那个神秘的“平方反比”规律都成立。电，这个曾经被认为是流体、是火、是神秘精气的玩意儿，终于被锁死在了一个简单的数学关系里：

F=kq1q2/r²。

不仅如此

如果库仑只做到了这一步，他已经可以名垂青史了。但他没有停。

他是个严谨得可怕的人。他知道漏电是个大问题。为了证明他的数据是可靠的，他在论文里花了大量篇幅讨论漏电。他计算了空气湿度的影响，他测量了电荷随时间的衰减率。他实际上是顺便创立了“漏电学”。

他告诉大家，他在做那几次关键读数的时候，电荷只泄露了不到五十分之一。这对于那个时代的仪器来说，简直是奇迹。

然后，他又把目光投向了磁。

磁铁和电荷一样，也是同性相斥，异性相吸。磁力是不是也遵循同样的规律？

库仑再次调整了他的扭秤。这次悬挂的不是麦秆，而是磁针。

结果毫无悬念。磁力也遵循平方反比定律。

直到这一刻，物理学的大图景才真正拼合起来。万有引力、电力、磁力，这三种主宰宏观世界的长程力，竟然共享着同一个数学骨架。

1785 年到 1787 年，库仑向法国皇家科学院提交了一系列回忆录。这些文件不像以前那些充满了文学修饰的观察报告，它们是冷冰冰的、充满数据和计算的工程文档。

但正是这些枯燥的文档，宣告了电磁学定性时代的结束，定量时代的开始。

沉默的基石

库仑定律发表后，并没有像某些科学发现那样立刻引起轰动。没有游行，没有烟花。

事实上，当时还有很多人不相信。有人怀疑扭秤的精度，有人觉得电荷在球表面的分布不均匀会影响结果。德国有些科学家甚至试图重复他的实验但失败了——因为他们没有库仑那双稳定的手，也没有他在马提尼克岛练就的对材料特性的深刻直觉。

但是，真理有它自己的惯性。

随着时间的推移，越来越多的人学会了使用扭秤。数学家们，像泊松和拉普拉斯，看到了库仑定律的美妙之处。因为这个定律和万有引力太像了，所以牛顿力学里发展出来的那套强大的数学工具——微积分、势论——可以直接照搬到电学里来。

根本不需要重新发明数学。只需要把质量 m 换成电荷 q，引力常数 G 换成库仑常数 k，一切都顺理成章。

之后的几十年里，电学的发展速度快得惊人。奥斯特发现了电生磁，安培发现了电流之间的力，法拉第看见了场，麦克斯韦最后把它们统统打包进了一组方程。

但所有这一切，始于那个玻璃罐子。

始于那根细细的银丝。

始于查尔斯·奥古斯丁·德·库仑盯着那个旋转的麦秆，在心里默默计算角度的那一刻。

他没有发明电，他没有发明电池，他甚至没有解释电到底是什么。他所做的，只是测量。

但在科学里，测量就是理解。只有当你能测量它，能用数字表达它时，你才真正了解了它。