由法拉第阻抗实验由于正弦扰动的幅值很小，可以用线性化的i-η，按照电子学的电流习惯，可重新写为

*O – CR)+ i/i]因此

ct0β=RT∗（3）

R∗（4）

R-1/ωC=R=RT0因此，和Cs电桥法以下关系。如图1所示。

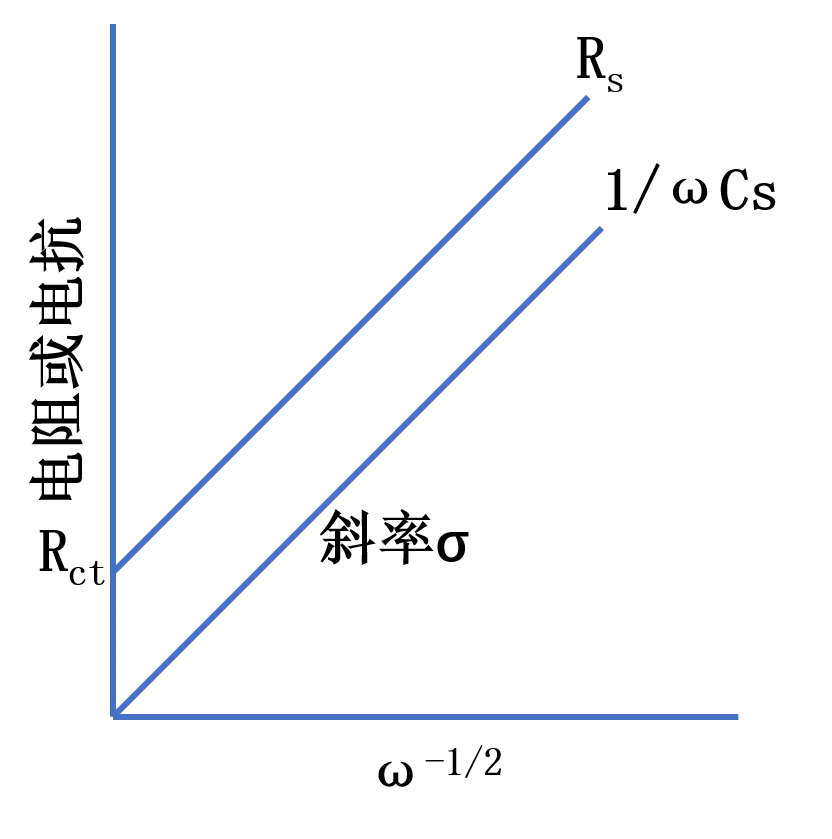
ss方程式（5）表明，原则上由一个频率得到的数据可以求出i。然而因为等效电路实际上反映的就是体系的行为，并没有实验的保证。例如，式R=R+σ1/2s1/2ss–1/2R作图的截距应是R，从它可以求出i。外推的截距相当于频率无限大时确定的特性性能。因为时间很短，。由于表面浓度永不会偏离平均值很多，因此，惟有电荷转移动力学支配着电流。

ctR=RT/nFi（7）

0cts1/2法拉第阻抗只是Warburg阻抗值Z=（2/ω）σ（8）

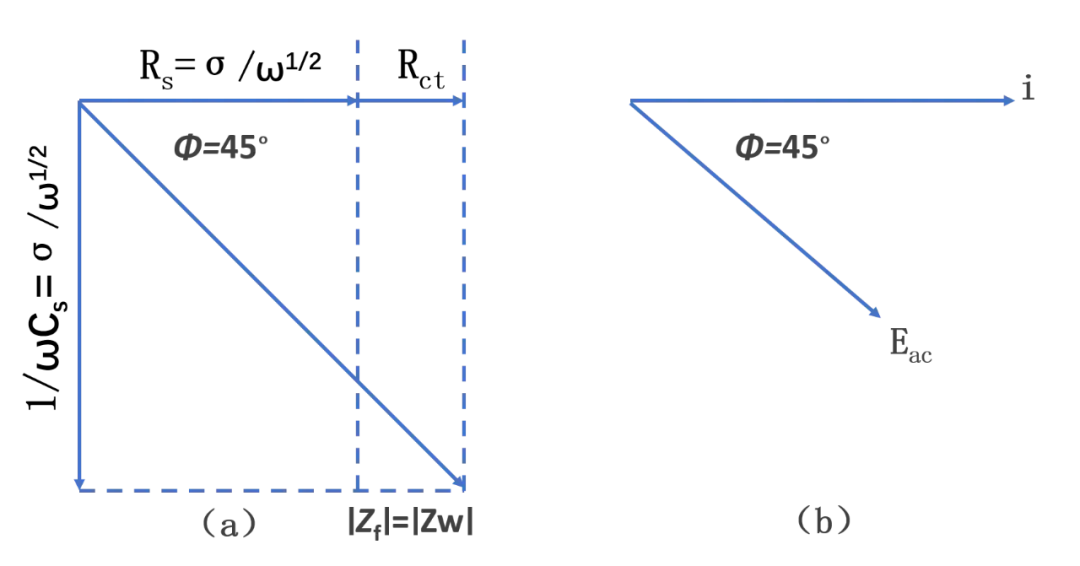
由于这是适用于任意电极反应的物质传递阻抗，所以它是一个最小的阻抗。如果动力学是可观察到的，那么另一因素R就要有贡献，Z必定较大，正如图3（a）描述的那样。

激励信号Eac。如果异相氧化还原过程很迟缓，则R和Z相当大，以致只有很小的电流交流分量，并且，检测的极限决定用这种方法可测定的速率常数的低限。

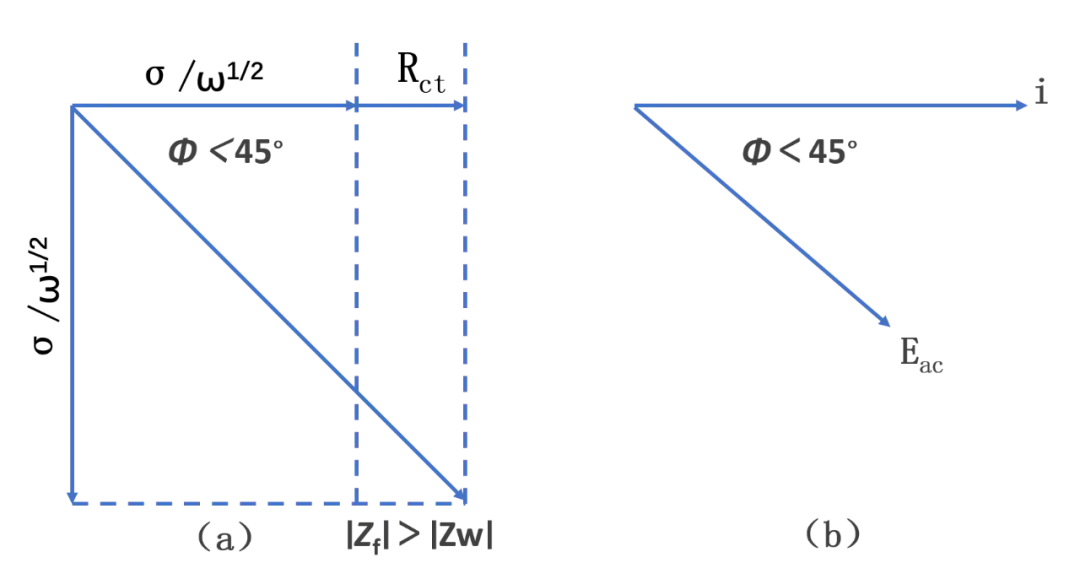
ct无论该比值较大还是较小，都意味着其中一种反应物的浓度很低，因此σ和Z必然大。此时，电流对交流扰动Eac的响应较小，原因在于。

在接近标准电势E⊖时，Zf预期最小种效应也预示着交流伏安曲线的响应形状。

在可逆情况下，R=0，因此φ=45°或π/4准可逆体系显示出R>0，因此φ→∞。但是，这样反应就很迟缓，在常规阻抗测量中也总是有小的交流电流流过。

ctacac相敏检测器（即锁相放大器）以Eac。这个特点在交流伏安法中作为区分充电电流的基础是特别有用的。

当电荷转移动力学证明它们自身在化学上是可逆的n电子体系，在这种情况下可以以图3中的关系讨论。

电化学阻抗谱学

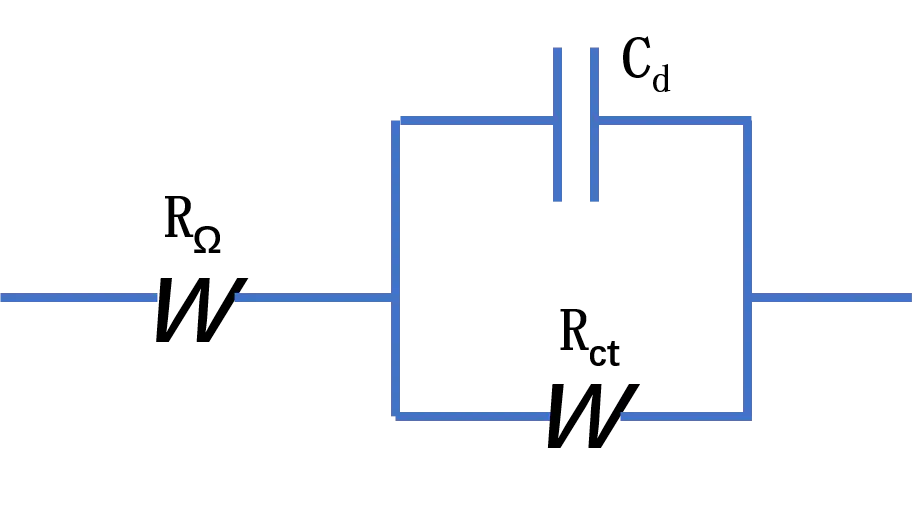
Ωd在给定的频率下，和双电层电容（或ZRe和ZIm）图4. 电解池的等效电路。

实验测定电解池的阻抗，但必须没有电活性电对ΩdBB更直接的方法涉及具有频率变量的总阻抗Z=R−j/（ωC）=Z−jZ方法研究。从变量中可以直接分离出R、C、R和C。也可以研究总阻抗Z=R−j/（ωC）=Z−jZ随频率的变化。、Cd和Cs电化学阻抗谱法是基于在电气工程电路分析中所用的方法，它处理复平面中总阻抗变化。可以将该方法用于标准体系中。

BBReBImBReZ=BR+s22这里A=（C/C）+1，B=ωRC。同理，

ImB2ds22将R和C简化，可得

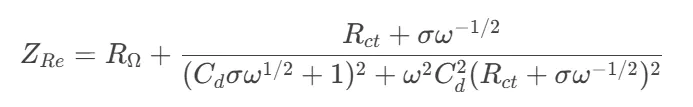
（2.4）

ImRe（1）低频极限：随着ω→0，函数（2.3）和函数（2.4）趋于其极限形式：

ReΩct–1/2Zσω+2σC（2.6）

Z=Z-R-R+2σC（2.7）

ImReΩct2dReImct图5. 低频下的阻抗图。

ct。阻抗是Z=R-j（R/（RCω-j））（2.8）。

它有如下的组分

ReΩct22RctZ=ωCRct22Rct上述两式中消除ω后得到

ReΩct22=（R/2）（2.11）

ImReReΩctImct图7. 图6中等效电路的阻抗面图。

d所有的电流均为充电电流，所看到的阻抗是欧姆电阻。dlmd因此，电流流动主要是通过R和R，（3）真实体系的应用图8是一个实际的阻抗在复平面的作图，它结合了上述两种极限情况的特点。

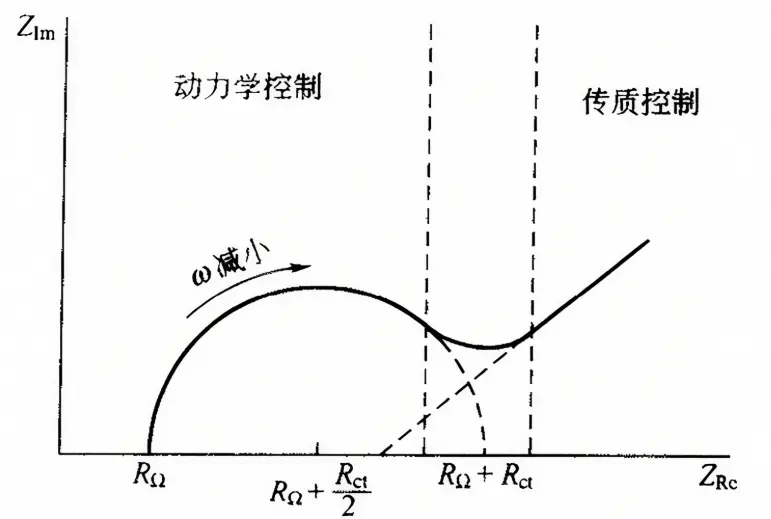
然而，对于任意给定的体系，上述两个区域（电荷转移与传质控制区）的界限往往并不明显。其决定性因素在于电荷转移电阻 Rct若一个化学体系动力学过程较慢，其 Rct 值较大，可能仅在较窄的频率范围内显示出物质传递的重要性在另一极端情况下，在几乎整个相关的 σ 范围内，Rct 图9. 实际化学体系的阻抗平面图。

用法拉第阻抗法测定k°的界线

（1）上限：ctsct1/2oR*=CRo1/2u7−1–520sdsΩ（2）下限：ccdctd0d2*–2–1d20—6