1948 年，一位名叫克劳德・香农的工程师，在《贝尔系统技术期刊》上发表了一篇题为《通信的数学理论》的论文。这篇论文篇幅不长，却彻底改变了人类对信息的认知，开创了一门全新的学科 —— 信息论。

从此，通信、计算机、互联网、人工智能、密码学等领域都迎来了爆发式发展。今天的5G网络、智能手机、云计算、流媒体服务、在线支付、人工智能助手，背后都离不开香农信息论的支撑。

香农的信息论把 “信息” 这个模糊的概念，变成了可以量化、可以计算、可以优化的数学工具；它回答了通信领域的核心问题：如何在有限的带宽里，以尽可能高的速度、尽可能低的误差传递信息。

信息到底是什么？

在香农之前，人们对 “信息” 的理解很模糊。有人觉得信息是 “有意义的消息”，有人觉得是 “有用的知识”，还有人觉得是 “未知的内容”。但这些定义都太主观，没法进行科学的分析和计算。

比如，“今天会下雨” 这句话，对农民来说可能是重要信息，对天天待在室内的人来说可能无关紧要；“地球是圆的” 这句话，对古人来说是颠覆性的信息，对现代人来说却是常识。如果信息的价值因人而异、因时而异，那我们怎么能建立一套统一的通信理论，指导工程师设计高效的通信系统？

香农的天才之处，在于他给出了一个客观、普适的信息定义：信息是用来消除不确定性的东西。

它把信息从主观的 “意义” 层面，拉到了客观的 “概率” 层面。不管一条消息有没有意义、对谁有用，只要它能减少我们对某个事件的不确定性，它就包含信息；减少的不确定性越多，包含的信息量就越大。

比如，有一个问题：“掷一枚均匀的硬币，正面朝上还是反面朝上？” 在没有任何信息的情况下，要你猜，你对这个问题的不确定性是最大的 —— 正面和反面的概率各占50%(排除硬币立起来的情况)。如果有人告诉你 “正面朝上”，这个消息就消除了我们的全部不确定性，所以它包含的信息量是最大的。

再比如，“今天是星期一” 这句话，对知道今天是周末的人来说，不确定性已经很小（知道是周六或周日），所以这句话带来的信息量就很小；但对完全失忆、不知道日期的人来说，不确定性很大（可能是一周七天中的任何一天），所以这句话带来的信息量就很大。

香农不仅定义了信息，还发明了 “信息量” 的计算单位 —— 比特（bit）。比特是二进制单位，只有 0 和 1 两种状态，是信息的最小单位。

具体来说，如果一个事件有 n 种等可能的结果，那么消除这个事件的不确定性所需要的信息量（即该事件的信息量）为：H = log₂n（log 以 2 为底 n 的对数）。

比如：

掷一枚均匀的硬币，有 2 种等可能结果，信息量 H = log₂2 = 1 比特；

掷一个均匀的骰子，有 6 种等可能结果，信息量 H = log₂6 ≈ 2.58 比特；

从 26 个英文字母中随机选一个，有 26 种等可能结果，信息量 H = log₂26 ≈ 4.7 比特。

这个公式看似简单，意义却很大。它意味着，信息不再是模糊的感觉，而是可以精确测量的，就像长度可以用米来衡量、重量可以用千克来衡量一样。

更重要的是，这个定义和计算方法，不依赖于消息的内容和接收者的主观感受，完全是客观的。不管是文字、声音、图像，还是其他形式的信息，都可以用比特来量化。既然信息可以量化，那通信系统的 “传输能力”“传输效率” 就都可以用数学来描述和优化了。

香农极限

在香农之前，通信领域的工程师不知道通信系统的性能有没有上限。为了提高通信速度，他们不断增加信号功率、改进编码方式，但效果越来越不明显，还经常出现信号失真、误差率上升的问题。

比如，早期的电报系统，只能通过莫尔斯电码传递简单的文字，速度很慢；后来的电话系统，虽然能传递声音，但距离越远，噪声越大，通话质量越差；无线电广播和电视信号，也经常受到干扰，出现雪花、卡顿。

工程师们不知道，他们是不是在做 “无用功”—— 有没有可能，无论怎么改进技术，通信速度都有一个无法突破的极限？如果有，这个极限是多少？

香农在《通信的数学理论》中，给出了这个问题的答案 —— 香农信道容量公式（也叫香农极限）：

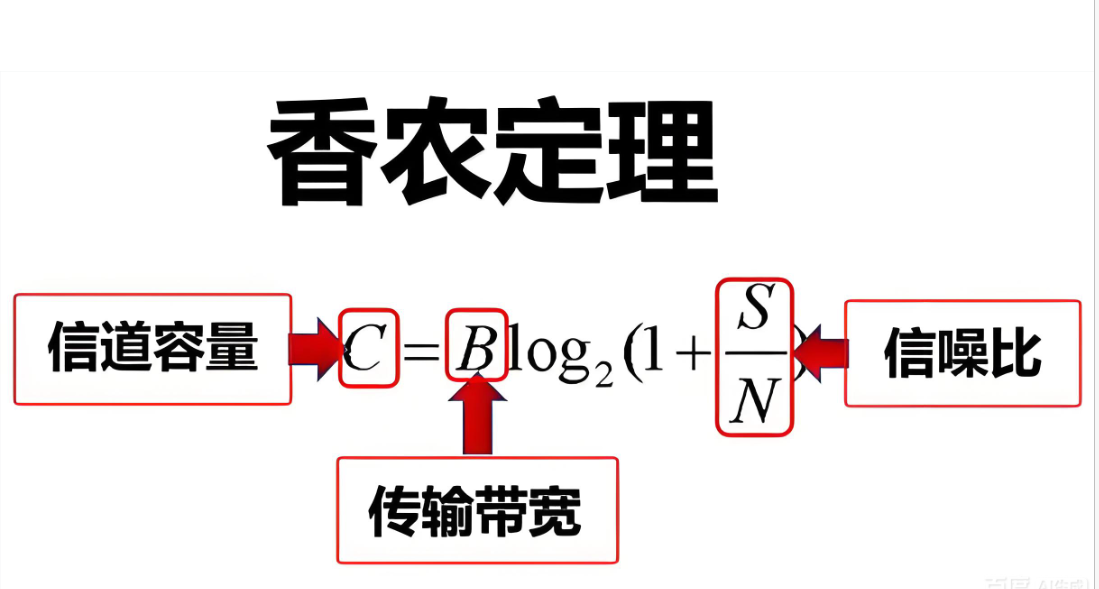
C = B log₂(1 + S/N)

其中，C 是信道容量（单位：比特 / 秒），代表信道在单位时间内最多能可靠传输的信息量；B 是信道带宽（单位：赫兹），代表信道能传输的频率范围；S/N 是信噪比，代表信号功率和噪声功率的比值。

这个公式说明了：任何通信信道都有一个最大传输速率（香农极限），这个极限由信道带宽和信噪比决定。

比如，一条带宽为 1MHz、信噪比为 30dB（S/N≈1000）的信道，根据香农公式计算，其信道容量 C = 1×10⁶ × log₂(1+1000) ≈ 1×10⁶ × 10 = 10⁶比特 / 秒（1Mbps）。这意味着，在这条信道上，最多能以 1Mbps 的速率可靠传输信息。如果想把传输速率提高到 2Mbps，无论采用什么编码方式，都会出现大量的传输错误。

香农极限的意义

香农极限的提出，彻底改变了通信领域的研究方向。

在香农之前，工程师们不知道通信的极限在哪里，只能盲目地尝试各种技术，浪费了大量的时间和资源。香农极限的提出，工程师们不再是无限制地追求传输速率，而是在香农极限范围内，寻找最优的编码方式和传输技术，实现接近极限的传输效率。

比如，在香农公式提出后，人们开始专注于研发高效的纠错编码技术，让信息在传输过程中即使受到噪声干扰，也能通过编码纠错，保证传输的可靠性。这些技术的研发，都是以香农极限为目标的。

香农公式还揭示了在信道容量不变的情况下，带宽和信噪比可以相互替代。

举个例子，如果信道带宽不足，可以通过增加信号功率（提高信噪比）来弥补，从而保持信道容量不变；反之，如果信号功率受限，可以通过增加带宽来弥补，同样能保持信道容量不变。

这种权衡关系，为通信系统的设计提供了极大的灵活性。比如，5G 网络采用了 “大规模天线”“超密集组网” 等技术，通过增加带宽来提高信道容量，同时避免了过度增加信号功率导致的能耗问题；而卫星通信由于传输距离远、信号衰减严重（信噪比低），则需要采用更大的带宽和更高效的纠错编码技术，才能保证通信质量。

从 2G、3G、4G 到 5G，每一代移动通信技术的升级，本质上都是在不断接近香农极限。

比如，2G 网络的传输速率约为 10kbps，远低于香农极限；3G 网络的传输速率约为 1Mbps，开始接近部分信道的香农极限；4G 网络的传输速率约为 100Mbps，进一步逼近香农极限；5G 网络的传输速率可达 10Gbps，已经非常接近香农极限在高频段的理论值。(说明：香农极限是特定信道条件下的理论值)

纠错编码

在通信过程中，噪声是不可避免的。无论是电线中的电流干扰、空气中的电磁辐射，还是设备本身的电子噪声，都会导致信号失真，让接收方收到错误的信息。

在香农之前，人类应对噪声的方法很简单：要么增加信号功率（让信号盖过噪声），要么减少传输距离（降低噪声干扰）。但这两种方法都有局限性 —— 增加信号功率会消耗更多能量，还可能造成干扰；减少传输距离则限制了通信的范围。

香农在信息论中提出了一个颠覆性的观点：噪声并不可怕，只要采用合适的编码方式，就能在有噪声的信道中实现可靠通信。这一观点，直接催生了 “纠错编码” 技术的诞生。

纠错编码的基本原理很简单：在发送信息时，额外添加一些 “冗余信息”，这些冗余信息与原始信息存在一定的逻辑关系；接收方收到信号后，可以通过这些冗余信息检测出传输过程中出现的错误，并自动纠正。

比如，发送方要发送 “1010” 这个 4 位二进制信息，为了实现纠错，可以在后面添加 1 位冗余位，使得整个编码的 “1” 的个数为偶数（这种编码方式叫 “偶校验码”）。那么，“1010” 就会变成 “10100”（其中最后一位 “0” 是冗余位，整个编码中 “1” 的个数是 2，为偶数）。

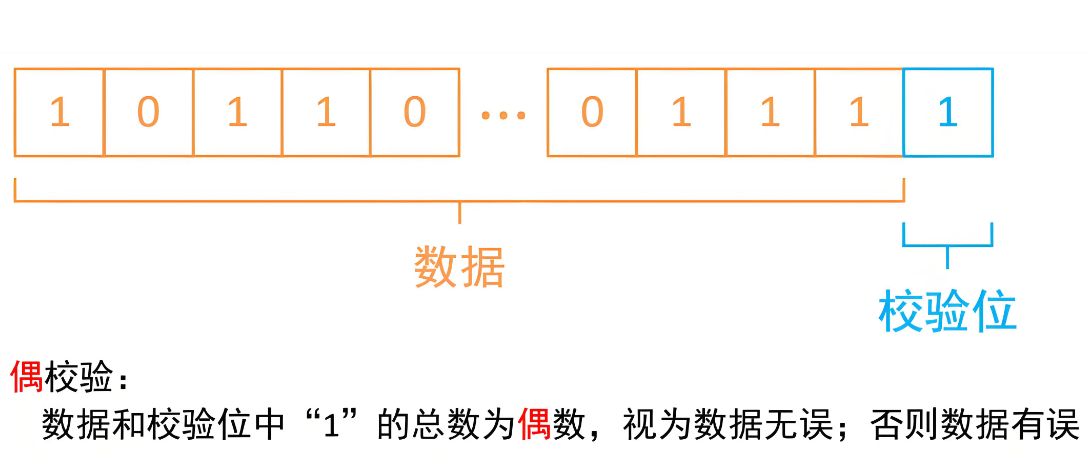
如果在传输过程中，其中一位发生错误（比如变成 “10110”），接收方会发现编码中 “1” 的个数是 3（奇数），从而判断出传输过程中出现了错误。但偶校验码只能检测出 1 位错误，无法纠正错误，也无法检测 “1 的个数不变但位置错位” 的错误。

但是香农的贡献在于，他从理论上证明了：存在一种 “理想编码”，能够在有噪声的信道中，以接近香农极限的速率传输信息，同时让错误率无限接近于零。这种理想编码，就是通过添加适量的冗余信息，来对抗噪声的干扰。

香农虽然证明了理想编码的存在，但并没有给出具体的编码方案。在他之后，工程师们围绕 “接近香农极限的纠错编码” 展开了研究，推动了纠错编码技术的不断发展。

用更少的比特传递更多的信息

除了通信和纠错，香农信息论还为数据压缩技术奠定了基础。数据压缩的核心目标，是在不丢失关键信息的前提下，用最少的比特数表示数据，从而节省存储空间和传输带宽。

比如，一张未经压缩的高清图片，大小可能有几十MB，传输和存储都很不方便；经过压缩后，大小可能只有几MB甚至几百KB，却依然能保持清晰的画质。我们常用的 JPEG图片格式、MP3音频格式、MP4视频格式，都是数据压缩技术的应用。

香农信息论中的 “信源编码定理”，为数据压缩提供了理论依据。信源编码定理指出：任何信源都存在一个最小的编码速率（称为 “信源熵率”），在这个速率下，能够实现无失真压缩；如果编码速率低于信源熵率，就无法实现无失真压缩。

信源熵是香农提出的另一个核心概念，它用来描述信源的不确定性，也就是信源产生信息的平均速率。信源熵的计算公式与信息量类似：H(X) = -ΣP (x) log₂P (x)，其中 P (x) 是信源发出符号 x 的概率。

信源熵的物理意义是：为了无失真地表示信源发出的每一个符号，平均需要的比特数。也就是说，信源熵是无失真数据压缩的 “极限”—— 无论采用什么压缩算法，都无法将编码速率降低到信源熵以下，否则就会出现信息丢失。

比如，英语字母的出现概率是不均匀的：“e” 出现的概率约为 12%，“t” 约为 9%，“a” 约为 8%，而 “z”“q” 等字母出现的概率不足 1%。根据信源熵的计算公式，去掉冗余度后的英语字母的信源熵约为 4.03 比特 / 字母。这意味着，在无失真的情况下，每个英语字母最少可以用 4.03 比特来表示。

这就是为什么数据压缩技术能有效减少数据量 —— 通过利用信源符号的概率分布不均匀性，给出现概率高的符号分配更短的编码，给出现概率低的符号分配更长的编码，从而降低平均编码长度，接近信源熵的极限。

数据压缩的影响

如果没有数据压缩，会是什么样子：

如果没有压缩技术，一张高清图片的传输可能需要几分钟，视频通话、在线直播等服务根本无法实现；一部高清电影需要几十GB甚至上百GB的存储空间；手机传输数据的流量消耗会大幅增加，5G网络的高速率也无法充分发挥作用；

游戏、动漫、电影等数字内容的制作和传播成本会大幅上升，数字娱乐产业也无法发展到今天的规模。

可以说，香农的信源编码定理，为数据压缩技术提供了理论基础，而数据压缩技术则为数字媒体产业的发展提供了可能。

信息论影响多个学科

计算机：

计算机的内存、硬盘等存储设备，本质上是通过二进制（0 和 1）来存储信息的，而二进制的设计正是基于香农的比特概念。

计算机网络的核心是数据传输，香农的信道容量公式和纠错编码理论，是网络协议设计的核心依据。比如，TCP/IP 协议中的流量控制、拥塞控制，都是为了在网络信道中实现高效、可靠的数据传输。

很多计算机算法的设计都借鉴了信息论的思想。比如，决策树算法通过计算 “信息增益”（基于信息熵）来选择最优的分裂节点，提高算法的效率；机器学习中的特征选择，也常用信息熵来衡量特征的重要性。

AI：

机器学习模型的训练过程，本质上是最小化 “预测值” 和 “真实值” 之间的信息差距。信息论中的 “交叉熵”“KL 散度” 等概念，是机器学习模型损失函数的核心。

深度学习中的神经网络，本质上是一个复杂的信息处理系统。信息论可以用来分析神经网络的信息传输效率、过拟合问题等。

强化学习中的 “探索与利用” 问题，本质上是信息获取与收益最大化的权衡。信息论中的 “互信息” 概念，可以用来衡量智能体对环境的了解程度，指导智能体的探索策略。

比如，我们常用的大语言模型，它的训练过程中使用的交叉熵损失函数，就是基于香农的信息论思想；模型的优化过程，也是在不断减少预测结果与真实结果之间的信息差距。

密码学：

香农在 1949 年发表的《保密系统的通信理论》中，将密码学纳入了信息论的框架。他提出了 “完美保密” 的概念：如果密文的信息量与明文的信息量无关，那么这个保密系统就是完美保密的。这一概念为对称加密算法的设计提供了理论依据。

信息论还为密钥长度的设计提供了指导。香农证明，要实现完美保密，密钥的长度至少要等于明文的长度。这一结论直接影响了现代密码学中密钥长度的选择，比如 AES 加密算法的密钥长度为 128 位、192 位或 256 位，就是为了保证加密的安全性。

网上购物、在线支付时使用的加密技术，背后都离不开香农信息论的支撑。

生物学：

DNA 由 A、T、C、G 四种碱基组成，这四种碱基的排列顺序承载了生命的遗传信息。信息论中的熵、互信息等概念，可以用来量化遗传信息的含量、遗传变异的程度等。

基因表达的过程，本质上是遗传信息的转录和翻译过程。信息论可以用来分析基因表达调控网络的信息传输效率，理解生命系统的复杂性；

生物的进化过程，本质上是遗传信息的变异和选择过程。信息论可以用来衡量进化过程中信息的增益和损失，为进化生物学的研究提供新的方法。

比如，科学家们通过计算 DNA 序列的信息熵，发现不同物种的 DNA 序列熵存在差异，这种差异反映了物种的进化程度和遗传多样性。

经济学：

经济学中的很多问题，本质上是信息不对称情况下的决策问题。信息不对称是指交易双方掌握的信息不一致，这会导致市场失灵。信息论中的信息熵、互信息等概念，可以用来量化信息不对称的程度。

博弈论中的很多模型，都涉及到信息的传递和决策。信息论可以用来分析博弈过程中信息的价值，指导参与者的决策。

金融市场中的投资者决策，本质上是基于信息的概率判断。信息论可以用来分析金融市场的信息效率。

香农的信息论之所以能跨界影响多个学科，是因为它揭示了信息的本质规律，而信息是自然界、人类社会和技术系统中普遍存在的现象。无论是通信、计算机、人工智能，还是生物学、经济学，只要涉及到信息的传递、处理和利用，都可以用信息论的思想和方法来分析。

在香农之前，人们看待世界的方式主要是“物质” 和 “能量”：比如，汽车是由钢铁等物质组成的，它的运动需要消耗汽油等能量；灯泡是由玻璃、灯丝等物质组成的，它的发光需要消耗电能。

香农告诉我们，除了物质和能量，“信息” 也是构成世界的基本要素。然界的生命演化、人类社会的沟通交流、技术系统的运行，都离不开信息的传递、处理和利用。

香农的信息论之所以牛，是因为它让人类能够用信息的视角来看待这一切。